Základní pojmy:
Klikovým mechanismem rozumíme sestavu klikového hřídele, ojnice a pístu. Na první pohled jednoduchý pohyb je poněkud složitější
a stojí za rozbor pro lepší pochopení podstaty věci. Kliková hřídel je zalomená hřídel uložená na hlavních ložiskách které jsou
osou rotace klikového hřídele. Počet zalomení závisí na počtu a uspořádání válců (podrobně popsáno dále).
Ojnice spojuje rameno kliky s pístem. Část ojnice uložená na klikové hřídeli se nazývá hlava ojnice a je buď dělená nebo vcelku.
Tato část vykonává spolu s ojničním čepem (na kterém se otáčí) rotační pohyb, který má opačný směr než pohyb klikové hřídele. Druhý
konec ojnice -oko ojnice- je uloženo na pístním čepu, který prochází pístem a vykonává translační (posuvný) pohyb. Rozložením
ROTAČNÍHO pohybu nám vznikne sinusová funkce, která platí pouze pro ojniční čep. Pohyb pístu v závislosti na natočení klikové
hřídele NENÍ tedy jednoduchou sinusovou funkcí a tudíž neplatí, že polovina natočení klikové hřídele odpovídá polovině zdvihu pístu.
Toto by platilo pouze za předpokladu, že by délka ojnice byla nekonečná.
Pro další výpočty a vysvětlení si zavedem poměr λ (lamda, která však nemá nic společného s lambdou-součinitelem přebytku vzduchu).
Jedná se o poměr délky ramene kliky a délky ojnice. λ=r/l Běžně je toto číslo kolem 0,2-0,4 a jakožto každý poměr je bezrozměrnou
jednotkou.
Kinematika:
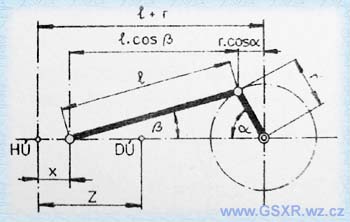
Dráha pístu:
Dráhu uvažujeme v závislosti na natočení klikového hřídele. Píst má dvě uvratě - dolní (DÚ) a horní (HÚ). Vzdálenost mezi HÚ a DÚ je zdvih,
plocha pístu krát zdvih je zdvihový objem. Délka ramena kliky určuje polovinu zdvihu. Tato hodnota je u motoru těžko měnitelná a tak se
běžněji zvětšuje objem motoru zvětšením vrtání-větší průměr pístu. Bohužel i ve skriptech se objeví chyba a chvilku trvalo než jsem se dopracoval
správnýho vzorce
x = r. ( 1 + 1/4λ - cosα - 1/4λ.cos(2α) ) [m]
r = rameno kliky [m]
l = délka ojnice [m]
Jako příklad jsem vybral dva odlišné stroje. Nízkootáčkový jednoválec DR600 a vysokootáčkový čtyřválec GSX600F. Kompletní grafy a výpočty naleznete
v Excelu ZDE
Pro DR platí přibližně tyto hodnoty:
r=45mm, l=135mm, λ=0,33, zdvih=2×r=90mm
Pro GSX600F platí přibližně tyto hodnoty:
r=24,35mm, l=110mm, λ=0,22, zdvih=2×r=48,7mm
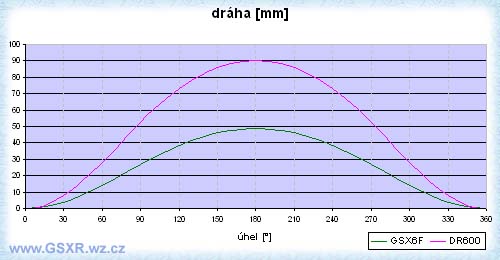
V grafu vidíme že ojnice je relativně dlouhá vůči zdvihu a odchylka od sinusové funkce není až tak velká. Ale přece jen je vidět, že pokud píst je v polovině své
dráhy (tzn. přesně v polovině zdvihu), kliková hřídel je natočená 80° od své horní uvratě. Při vyšších hodnotách λ se bude zvětšovat odchylka od sinusové
funkce. Na dráze pístu to není tak patrné jak na dalších měřených veličinách (rychlost, zrychlení). Teoreticky nekonečná ojnice způsobí chod pístu přesně dle funkce sinus.
Při ojnici dlouhé jako je rameno kliky je sice prakticky provoz nemožný, ale teoreticky by to znamenalo že při úhlu natočení kliky 90°z horní uvratě bychom byly již v
dolní uvrati. (kdo nevěří ať si vezme papír a kružítko)
Rychlost pístu:
Určuje nám opotřebení povrchu píst(kroužky)-válec. Tato rychlost je proměnná a jak si vysvětlíme dále mění se od 0 m/s do svého maxima,
které leží pod polovinou zdvihu. Rychlost tedy dostaneme derivací dráhy pístu (jednoduše řečeno derivace určuje rychlost změny a tedy pokud
máme křivku dráhy tak rychlost bude největší v místě kde je křivka nejstrmější).
v = r. ω( sinα + 1/2λ . sin2α ) [m/s]
ω = 2.π.n (n=otáčky/sec)
ω = úhlová rychlost
Vzhledem ke složitosti výpočtu (v dobách kdy nebyla technika) zavedl se střední pístová rychlost. Vychází z předpokladu, že považujem
rychlost pístu za konstantní. Dráhou pístu je zdvih a čas určený na tento pohyb je dán otáčkami motoru. 1 otáčka motoru nám určuje dva zdvihu
(píst jde shora dolů a pak opět nahoru).
vs = 2 . z . n [m/s]
z = zdvih [m]
n = ot/sec
Jak je vidět, střední pístová rychlost závisí na otáčkách, ale hlavně i na zdvihu motoru a mohou vzniknout překvapivé výsledky. Jako příklad
uvedu dva naprosto odlišné stroje. Vysokootáčkový motor Yamaha R6 a nízkootáčkový Suzuki Intruder 1600. U obou motorů použijem pro výpočet otáčky
maximálního výkonu.
Yamaha R6: vs = 2 . 44,5 . 10-3 . 13 000/60 = 19,28 m/s
Intuder: vs = 2 . 95 . 10-3 . 5 300/60 = 16,8 m/s
Pokud bychom Intrudera vytočili do 6090ot/min dostanem se na stejnou střední pístovou rychlost jako u motoru R6 který má víc jak 2×větší počet otáček.
Motocykly mají střední pístovou rychlost běžně do 20m/s. Nad touto rychlostí dochází k většímu opotřebení vlivem sdírání olejového filmu.
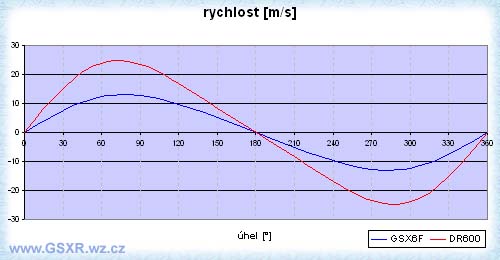
Rychlost pístu je už závislá na otáčkách, které jsem použil pro oba motory 5000 ot/min. Jak již bylo uvedeno, rychlost nezávisí pouze na otáčkách, ale i na
zdvihu motoru a tak DR má rychlejší píst ve stejných otáčkách než GSXF. Je potřeba si povšimnout i místa s maximální rychlostí a to asi v 70°natočení kliky od HÚ.
Tato skutečnost je jasná pokud si uvědomíme dráhu pohybu pístu. Berme, že klikový hřídel se otáčí konstantními otáčkami tzn. otočení 0°-90° musí trvat
stejnou dobu jako 90°-180°. Dráha pístu však není stejná. U DR to vychází 52,5mm a pak 37,5mm. Tyto dráhy pístu se dějí ve stejném časovém úseku a je na bíledni,
že delší dráhu musí urazit větší rychlostí aby to stihl za stejný čas.
Střední pístová rychlost je cca 60% maximální rychlosti (DR600: vs=15m/s, vmax=25m/s).
Zrychlení pístu:
Z Newtonova zákona nám vychází síla jako součin hmotnosti a zrychlení F = m . a. Tzn. že pokud chceme aby na součást působila malá síla (souvisí s opotřebením)
je nutné mít malé zrychlení nebo malou hmostnost součásti. Tato skutečnost se projevuje velmi silně i při návrhu ventilového rozvodu. Zrychlení je
všeobecně změna rychlosti. Pokud se tedy píst pohybuje mezi dvěmi polohami (DÚ a HÚ) mění se jeho rychlost a tím i jeho zrychlení. Stejně tak když
na motorce pojedeš po rovině úsek např. 100m musíš se prvně rozjet a změnit svou rychlost z 0 km/h, zrychlení bude velké a jak se budeš blížit do
poloviny dráhy přestaneš zrychlovat. Rychlost zde bude maximální a zrychlení malé. Od poloviny začneš rychlost snižovat (záporné zrychlení) až
snížíš rychlost opět na 0 km/h.
a = r. ω2( cosα + λ . cos2α ) [m/s]
ω = 2.π.n (n=otáčky/sec)
ω = úhlová rychlost
Po dosazení do vzorce nám vychází maximální zrychlení v případě kdy α = 0° nebo 180° tzn. píst je v DÚ nebo v HÚ. Naopak minimální zrychlení je v
případě, kdy je rychlost maximální. Odpovídá to tedy i našemu předchozímu příkladu s jedoucí motorkou.
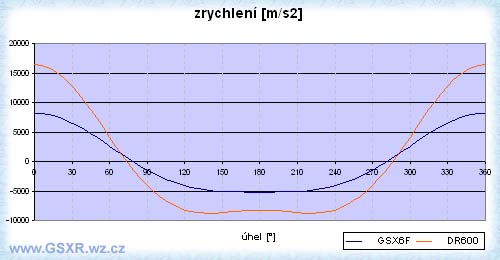
Vidíme, že naše předchozí úvaha není zcela korektní pro všechny hodnoty λ a to vlivem druhého výrazu rovnice cos2α. Sčítá se nám totiž funkce cos s periodou
360° a s periodou 180°. Čím tedy bude λ větší bude větší vliv na výsledek i cos2α. DR má λ=0,33 a GSXF má λ=0,22 a tudíž u DR vychází v DÚ menší
záporné zrychlení (tj. spomalení) než před dolní úvratí (v grafu je při 180° hrb směrem nahoru). Stojí i za povšimnutí vlivu zdvihu na velikost zrychlení.
Zrychlení je hlavní faktor určující sílu na dané těleso a dále je to hmotnost, kterou se snažíme taky snížit - např. kované písty a ojnice.
F=m.a síla je hmotnost × zrychlení. Z grafu je též vidět odlišnost zrychlení v HÚ a v DÚ a tak z hlediska setrvačných sil je ojnice více namáhána na tah než tlak (cca 1,8-2×).
Jak již bylo řečeno zrychlení je pro dané těleso hlavním faktorem pro velikost síly působící na těleso a tak síla má naprosto stejný průběh. Pokud si tedy v ojnici
představíme siloměr, který nám bude ukazovat velikost a směr síly (tah nebo tlak) tak při sledování grafu vidíme, že při rozběhu z HÚ je ojnice namáhaná na tah, cca v 75°
natočení klikové hřídele je zrychlení a tím i síla nulové a píst působí tlakem na ojnici, protože ta píst zpomaluje. Při překročení DÚ je ojnice stále namáhaná na tlak,
protože tlačí píst vzhůru, cca 105° za DÚ (75°před HÚ) máme sílu opět nulovou a píst vlivem setrvačnosti má tendenci pokračovat směrem vzhůru, ale ojnice jej brzdí a
tudíž je namáhaná na tah.
Dynamika:
Šikovný program který po zadání zdvihu a stupňů po kterých se má provádět výpočet
vyhodí polohu pístu v závislosti na natočení klikovky.
Související články:
Klikové ústrojí - popis jednotlivých částí (ojnice, ložiska, píst)
Oprava klikových hřídelů - způsoby oprav
Oprava ojnic - úhlování ojnic
autor: GSX-Roll